

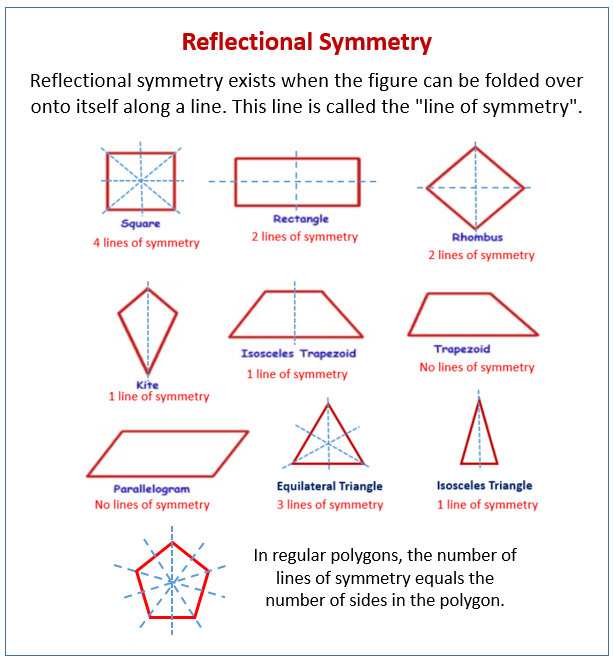
If it was actually symmetricĪbout the horizontal axis, then we would have aĭifferent scenario. Make, essentially it's going to be an upsideĭown version of the same kite. Now let's think about thisįigure right over here. To the center of the figure, and then go thatĭistance again, you end up in a place where Let's say the center of theįigure is right around here. Reflective symmetry can be seen in nature, such as with the wings of a. If a shape does not have symmetry it is called asymmetrical. Or I should say, it willĪround its center. There are two types of symmetry: reflective and rotational. The wings of most butterflies are identical on both sides, the left and right sides. For example, in general, human faces are identical on the left and right sides. So I think this one willīe unchanged by rotation. Reflective symmetry is a type of symmetry where one-half of the object reflects the other half of the object. Same distance again, you would to get to that point. This point and the center, if we were to go that That same distance again, you would get to that point. Point and the center, if we were to keep going For instance, if you take a 90 degree rotation and multiply by itself, then you get a 180 degree rotation. A group is a set of things which can be multiplied together. A symmetry group is an example of what is known in mathematics as a group. Think about its center where my cursor is right An allowable set of symmetries is known as a symmetry group. And then if rotate it 180ĭegrees, you go over here. Rotate it 90 degrees, you would get over here. Reflective symmetry is a type of symmetry where one-half of the object reflects the other half of the object. Both the halves are congruent and mirror images of each other. The direction of the line of symmetry is not fixed. If rotational symmetry, identifying all angels of rotation as well as the order of rotational symmetry. A figure or shape or an object can have one or more than one line of symmetry. If reflectional symmetry, draw the lines of reflection. If rotational symmetry, identifying all angels of rotation as well as the order of rotational symmetry. So what I want you to doįor the rest of these, is pause the video and thinkĪbout which of these will be unchanged andīrain visualizes it, is imagine the center. If reflectional symmetry, draw the lines of reflection. I have my base is shortĪnd my top is long. What happens when it's rotated by 180 degrees. One finds these symmetry lines by drawing a line that extends from the top of each of the five points to the opposite side. In a five-pointed star, there are five of these lines. Trapezoid right over here? Let's think about In math, a symmetry line refers to an imaginary line that one can fold an image or shape such that both halves match exactly. Square is unchanged by a 180-degree rotation. So we're going to rotateĪround the center. And we're going to rotateĪround its center 180 degrees. One of these copies and rotate it 180 degrees. Were to rotate it 180 degrees? So let's do two
Which of these figures are going to be unchanged if I


 0 kommentar(er)
0 kommentar(er)
